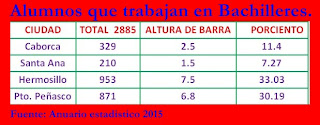
1.-Se suman todas las frecuencias en caso de que no aparescan en la tabla.
2.-Se expresan todas las frecuencias en porcentaje.
3.-Se multiplicanlas frecuencias porcentuales por el factor 3.6, la suma de estas medidas angulares debera ser de 360º.
4.-Se traza una circunferencia de radio albritario.
5.-Se traza un radio vertical y con el uso del transportador se trazan los grados del mayor al menor.
6.-En cada sector se escribe el porcentaje y se le anexa encabezado y pie sin olvidar de simbología.
Ejemplo: